概述
树是计算机中非常重要的一种数据结构,同时使用树这种数据结构,可以描述现实生活中的很多事物,例如族谱、单位的组织架构、等等。树是由n(n>=1)个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树。
树具有以下特点:
-
每个结点有零个或多个子结点;
-
没有父结点的结点为根结点;
-
每一个非根结点只有一个父结点;
-
每个结点及其后代结点整体上可以看做是一棵树,称为当前结点的父结点的一个子树;
树的术语
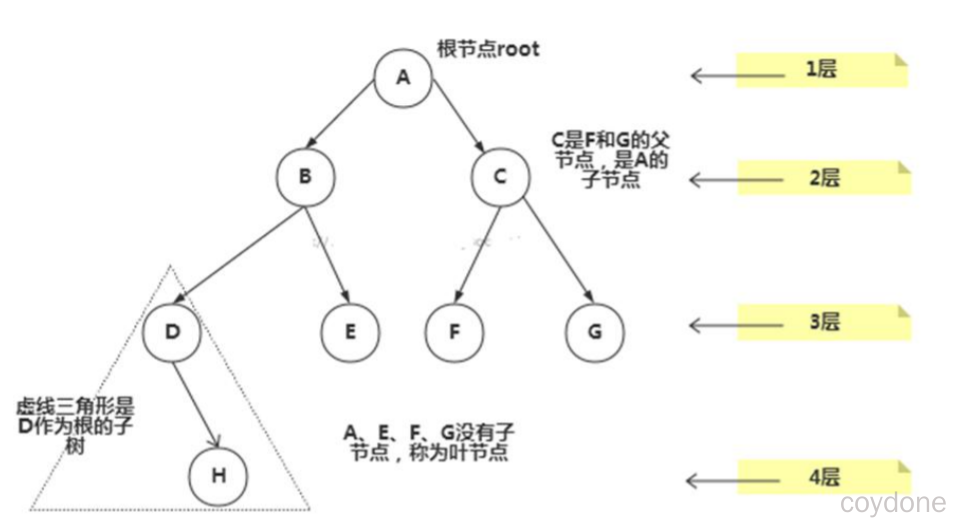
结点的度:一个结点含有的子树的个数称为该结点的度;
叶结点:度为0的结点称为叶结点,也可以叫做终端结点
分支结点:度不为0的结点称为分支结点,也可以叫做非终端结点
结点的层次:从根结点开始,根结点的层次为1,根的直接后继层次为2,以此类推
结点的层序编号:将树中的结点,按照从上层到下层,同层从左到右的次序排成一个线性序列,把他们编成连续的自然数。
树的度:树中所有结点的度的最大值
树的高度(深度):树中结点的最大层次
森林: m(m>=0)个互不相交的树的集合,将一颗非空树的根结点删去,树就变成一个森林;给森林增加一个统一的根结点,森林就变成一棵树。
孩子结点:一个结点的直接后继结点称为该结点的孩子结点。
双亲结点(父结点):一个结点的直接前驱称为该结点的双亲结点。
兄弟结点:同一双亲结点的孩子结点间互称兄弟结点。
二叉树
概述
二叉树就是度不超过2的树(每个结点最多有两个子结点)。
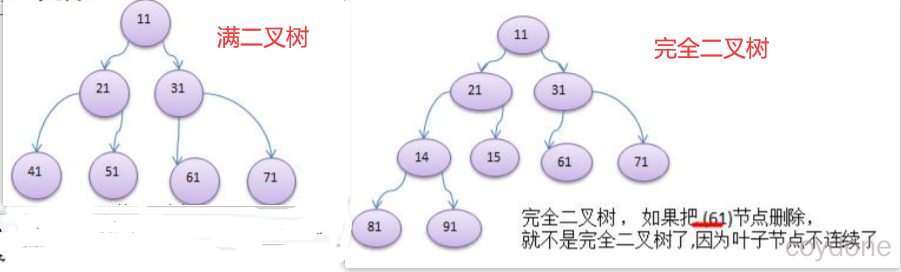
满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。
完全二叉树:叶节点只能出现在最下层和次下层,并且最下面一层的结点都集中在该层最左边的若干位置的二叉树。
二叉查找树(BST):是一种特殊的二叉树,相对较小的值保存在左节点中,较大的值保存在右节点中。
API设计
结点类
类名 Node<K,V>
构造方法 Node(K key, V value, Node left, Node right):创建Node对象
成员变量
public Node left:记录左子结点
public Node right:记录右子结点
public K key:存储键
public V value:存储值
二叉树
类名:BinaryTree<K,V>
构造方法:BinaryTree():创建BinaryTree对象
成员变量
private Node root:记录根结点
private int n:记录树中元素的个数
成员方法
public void put(K key,V value):向树中插入一个键值对
private Node put(Node x, K key, V val):在树x上添加一个键值对,并返回新树
public V get(K key):根据key,从树中找出对应的值
private V get(Node x, K key):从指定的树x中,找出key对应的值
public void delete(K key):根据key,删除树中对应的键值对
private Node delete(Node x, K key):删除树x上键为key的键值对,并返回新树
public int size():获取树中元素的个数
BST代码实现
插入方法put()实现思想:
-
如果当前树中没有任何一个结点,则直接把新结点当做根结点使用;
-
如果当前树不为空,则从根结点开始:如果新结点的key小于当前结点的key,则继续找当前结点的左子结点;如果新结点的key大于当前结点的key,则继续找当前结点的右子结点;如果新结点的key等于当前结点的key,则树中已经存在这样的结点,替换该结点的value值即可。
查询方法get()实现思想:从根节点开始,如果要查询的key小于当前结点的key,则继续找当前结点的左子结点;如果要查询的key大于当前结点的key,则继续找当前结点的右子结点;如果要查询的key等于当前结点的key,则树中返回当前结点的value。
删除方法delete()实现思想:
-
找到被删除结点;
-
找到被删除结点右子树中的最小结点minNode;
-
删除右子树中的最小结点;
-
让被删除结点的左子树成为最小结点minNode的左子树,让被删除结点的右子树称为最小结点minNode的右子树;
-
让被删除结点的父节点指向最小结点minNode。
//二叉查找树
public class BinaryTree<K extends Comparable,V> {
//记录根结点
private Node<K,V> root;
//记录树中元素的个数
private int n;
public BinaryTree() {
}
//向树中插入一个键值对
public void put(K key,V value) {
root = put(root,key,value);
}
//在树tree上添加一个键值对,并返回添加后的新树
private <K extends Comparable> Node<K,V> put(Node<K,V> tree, K key, V value) {
if (tree == null) {
//直接把新结点当成根结点使用
//个数+1
n++;
return new Node<>(key,value,null,null);
}
//比较key,新结点的key > 当前结点的key,继续找当前结点的右子结点
if (key.compareTo(tree.key) > 0) {
tree.right = put(tree.right, key, value);
} else if (key.compareTo(tree.key) < 0) {
// 新结点的key小于当前结点的key,继续找当前结点的左子结点
tree.left = put(tree.left, key, value);
} else {
// 新结点的key等于当前结点的key
tree.value = value;
}
return tree;
}
//根据key,从树中找出对应的值
public V get(K key) {
return get(root, key);
}
//从指定的树tree中,找出key对应的值
private V get(Node tree, K key) {
if (tree == null) {
return null;
}
// 如果要查询的key > 当前节点的key,则继续查找当前节点的右子结点
if (key.compareTo(tree.key) > 0) {
return get(tree.right, key);
} else if (key.compareTo(tree.key) < 0) {
// 如果要查询的key < 当前节点的key,则继续查找当前节点的左子结点
return get(tree.left, key);
} else {
// 要查找的key和当前结点的key相等,返回value
return (V) tree.value;
}
}
//根据key,删除树中对应的键值对
public void delete(K key) {
root = delete(root, key);
}
//删除树tree上键为key的键值对,并返回新树
private Node<K ,V> delete(Node tree, K key) {
if (tree == null) {
return null;
}
// 待删除的key > 当前节点的key,继续找当前节点的右子结点
if (key.compareTo(tree.key) > 0) {
tree.right = delete(tree.right, key);
} else if (key.compareTo(tree.key) < 0) {
tree.left = delete(tree.left, key);
} else {
// 待删除的key等于当前节点的key,说明当前结点就是要删除的结点
// 1. 如果当前结点的右子树不存在,则直接返回当前结点的左子节点
if (tree.right == null) {
n--;
return tree.left;
}
// 2. 如果当前结点的左子树不存在,则直接返回当前结点的右子节点
if (tree.left == null) {
n--;
return tree.right;
}
// 3. 当前结点的左右子树都存在
// 3.1 找到右子树中最小的结点
Node minNode = tree.right;
// 二叉查找树的左节点一定比右节点小,所以这里只需要遍历左节点
if (minNode.left != null) {
minNode = minNode.left;
}
// 到这里,就找到了当前节点右子树中最小的节点minNode
// 3.2 删除右子树中最小的节点
Node node = tree.right;
while (node.left != null) {
if (node.left.left == null) {
// 说明n的左节点就是我们要找的最小结点
node.left = null;
} else {
node = node.left;
}
}
// 到这里,最小结点已经被删除
// 3.3 让被删除结点的左子树成为最小结点的左子树。让被删除结点的右子树,成为最小结点的右子树
minNode.left = tree.left;
minNode.right = tree.right;
// 3.4 让被删除结点的父节点指向最小结点
tree = minNode;
// 个数-1
n--;
}
return tree;
}
//获取树中元素的个数
public int size() {
return n;
}
private static class Node<K extends Comparable,V> {
//存储键
public K key;
//存储值
public V value;
//记录左子结点
public Node left;
//记录右子结点
public Node right;
public Node(K key, V value,Node left, Node right) {
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
}
}
二叉树的遍历
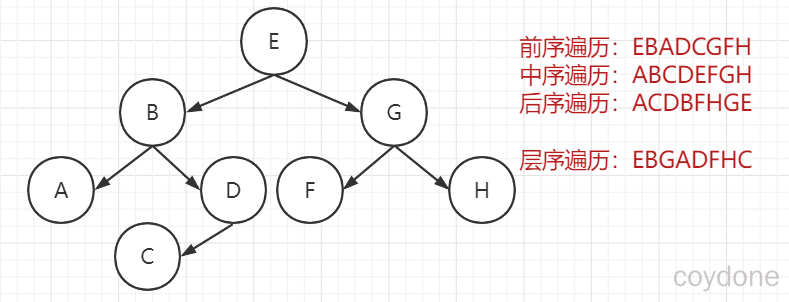
使用前序,中序和后序对下面的二叉树进行遍历。看输出父节点的顺序,就确定是前序,中序还是后序。
-
前序遍历:先输出父节点,再遍历左子树和右子树。
-
中序遍历:先遍历左子树,再输出父节点,再遍历右子树。
-
后序遍历:先遍历左子树,再遍历右子树,最后输出父节点。
层序遍历,就是从根节点(第一层)开始,依次向下,获取每一层所有结点的值。
前序遍历
//前序遍历
//1. 把当前结点的key放入到队列中;
//2. 找到当前结点的左子树,如果不为空,递归遍历左子树
//3. 找到当前结点的右子树,如果不为空,递归遍历右子树
public List preErgodic() {
List keys = new LinkedList();
preErgodic(root, keys);
return keys;
}
private void preErgodic(Node tree, List keys) {
if (tree == null) {
return;
}
// 1.把当前结点的key放入到List中
keys.add(tree.key);
// 2.找到当前节点的左子树,如果不为空,递归遍历左子树
if (tree.left != null) {
preErgodic(tree.left, keys);
}
// 3.找到当前结点的右子树,如果不为空,递归遍历右子树
if (tree.right != null) {
preErgodic(tree.right, keys);
}
}
测试
class Test {
public static void main(String[] args) {
BinaryTree<String,String> tree = new BinaryTree<>();
tree.put("E", "E");
tree.put("B", "B");
tree.put("G", "G");
tree.put("A", "A");
tree.put("D", "D");
tree.put("F", "F");
tree.put("H", "H");
tree.put("C", "C");
List list1 = tree.preErgodic();
System.out.println("前序遍历:");
list1.forEach(System.out::print);
}
}
中序遍历
//中序遍历
//实现步骤
//1. 找到当前结点的左子树,如果不为空,递归遍历左子树
//2. 把当前结点的key放入到队列中;
//3. 找到当前结点的右子树,如果不为空,递归遍历右子树
public List midErgodic() {
List keys = new LinkedList();
midErgodic(root, keys);
return keys;
}
private void midErgodic(Node tree, List keys) {
if (tree == null) {
return;
}
// 1.找到当前结点的左子树,如果不为空,递归遍历左子树
if (tree.left != null) {
midErgodic(tree.left, keys);
}
// 2.把当前结点的key放入到List中
keys.add(tree.key);
// 3.找到当前结点的右子树,如果不为空,递归遍历右子树
if (tree.right != null) {
midErgodic(tree.right, keys);
}
}
后序遍历
//后序遍历
//实现步骤:
//1. 找到当前结点的左子树,如果不为空,递归遍历左子树
//2. 找到当前结点的右子树,如果不为空,递归遍历右子树
//3. 把当前结点的key放入到队列中;
public List afterErgodic() {
List keys = new LinkedList();
afterErgodic(root, keys);
return keys;
}
private void afterErgodic(Node tree, List keys) {
if (tree == null) {
return;
}
// 1.找到当前结点的左子树,如果不为空,递归遍历左子树
if (tree.left != null) {
afterErgodic(tree.left, keys);
}
// 2.找到当前结点的右子树,如果不为空,递归遍历右子树
if (tree.right != null) {
afterErgodic(tree.right, keys);
}
// 3.把当前结点的key放入到List中
keys.add(tree.key);
}
层序遍历
//层序遍历
//实现步骤:
//1. 创建List,存储每一层的结点;
//2. 使用循环从队列中弹出一个结点:
// 2.1获取当前结点的key;
// 2.2如果当前结点的左子结点不为空,则把左子结点放入到队列中
// 2.3如果当前结点的右子结点不为空,则把右子结点放入到队列中
public List layerErgodic() {
// 创建一个队列,存储每一层的节点
ArrayQueue<Node> nodes = new ArrayQueue<>(n);
// 创建一个List,用于存储遍历的节点
List keys = new ArrayList();
// 将当前节点存储到nodes中
nodes.add(root);
// 遍历queue
while (!nodes.isEmpty()) {
// 出列
Node currentNode = nodes.remove(0);
// 把节点的key存入到keys中
keys.add(currentNode.key);
// 如果当前节点的左子节点不为空,则把左子节点放入到队列中
if (currentNode.left != null) {
nodes.add(currentNode.left);
}
// 如果当前节点的右子节点不为空,把右子节点放到队列中
if (currentNode.right != null) {
nodes.add(currentNode.right);
}
}
return keys;
}
最大深度问题
给定一棵树,请计算树的最大深度(树的根节点到最远叶子结点的最长路径上的结点数)。
实现步骤:
-
如果根结点为空,则最大深度为0;
-
计算左子树的最大深度;
-
计算右子树的最大深度;
-
当前树的最大深度=左子树的最大深度和右子树的最大深度中的较大者+1。
//计算整个树的最大深度
public int maxDepth() {
return maxDepth(root);
}
//计算指定树tree的最大深度
private int maxDepth(Node tree) {
if (tree == null) {
return 0;
}
// 计算左右子树的最大深度
int max = 0;
int leftMax = 0;
int rightMax = 0;
// 计算左子树最大深度
if (tree.left != null) {
leftMax = maxDepth(tree.left);
}
// 计算右子树最大深度
if (tree.right != null) {
rightMax = maxDepth(tree.right);
}
// 将二者较大的一方赋值给max。当前树的最大深度就是max+1
max = leftMax > rightMax ? leftMax + 1 : rightMax + 1;
return max;
}
折纸问题
需求:请把一段纸条竖着放在桌子上,然后从纸条的下边向上方对折1次,压出折痕后展开。此时 折痕是凹下去的,即折痕突起的方向指向纸条的背面。如果从纸条的下边向上方连续对折2 次,压出折痕后展开,此时有三条折痕,从上到下依次是下折痕、下折痕和上折痕。 给定一 个输入参数N,代表纸条都从下边向上方连续对折N次,请从上到下打印所有折痕的方向 例如:N=1时,打印:down;N=2时,打印:down down up。
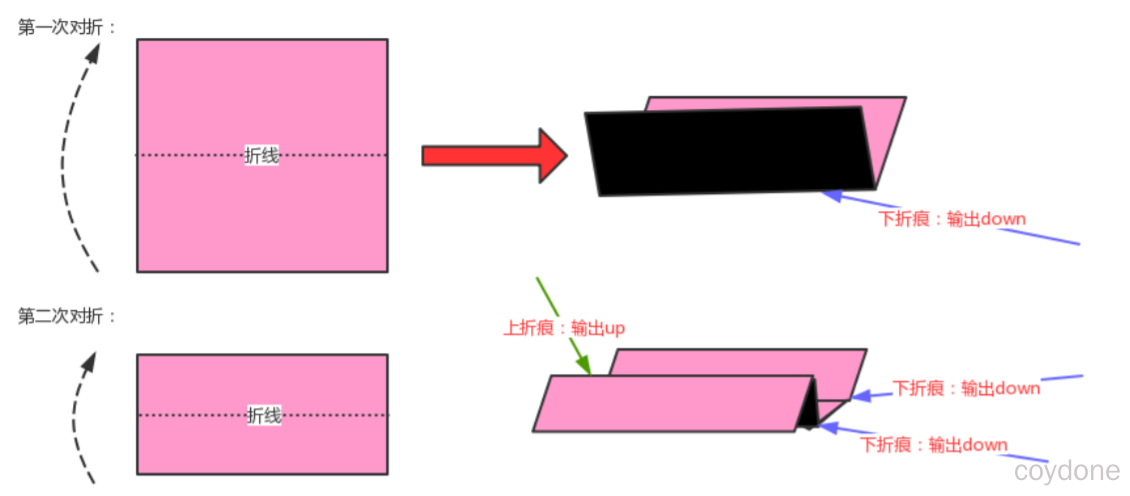
我们把对折后的纸张翻过来,让粉色朝下,这时把第一次对折产生的折痕看做是根结点,那第二次对折产生的下折 痕就是该结点的左子结点,而第二次对折产生的上折痕就是该结点的右子结点,这样我们就可以使用树型数据结构 来描述对折后产生的折痕。
这棵树有这样的特点:根结点为下折痕; 每一个结点的左子结点为下折痕;每一个结点的右子结点为上折痕;
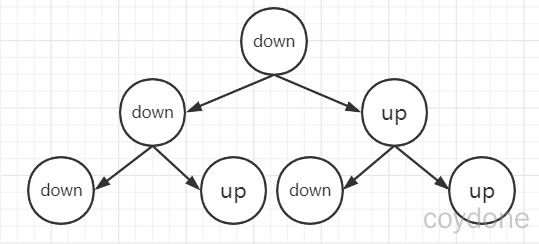
实现步骤:
1. 定义结点类
2. 构建深度为N的折痕(树结构)
3. 使用中序遍历,打印出树中所有结点的内容
构建深度为N的折痕树:
1. 第一次对折,只有一条折痕,创建根节点
2. 如果不是第一次对折,判断当前节点左右子树是不是空
3. 如果是空,就给当前节点构建一个左子树(down)和一个右子树(up)
4. 获取当前树的左右子树,重复第2步骤
public class PaperFold {
public static void main(String[] args) {
Node node = initTree(3);
print(node);
}
/**
* 使用中序遍历打印出所有的节点
* @param tree
*/
private static void print(Node tree) {
if (tree == null) {
return;
}
print(tree.left);
System.out.print(tree.item + ",");
print(tree.right);
}
/**
* 构建深度为N的折痕树
* @param n 需要构建的树的深度
*/
private static Node initTree(int n) {
// 根节点
Node root = null;
// 循环n次
for (int i = 0; i < n; i++) {
if (i == 0) {
// 第一次对折,创建根节点
root = new Node("down", null, null);
} else {
// 不是第一次
// 创建一个队列,将根节点存放到队列中
PaperQueue queue = new PaperQueue();
// 根节点入列
queue.enqueue(root);
// 遍历队列
while (!queue.isEmpty()) {
// 从队列中取出一个节点
Node node = queue.dequeue();
// 3. 获取当前树的左右子树,重复第2步骤
Node left = node.left;
Node right = node.right;
// 判断左右子树是否为空,如果不为空,存入队列
if (left != null) {
queue.enqueue(left);
}
if (right != null) {
queue.enqueue(right);
}
// 1. 如果不是第一次对折,判断当前节点左右子树是不是空
if (node.left == null && node.right == null) {
// 2. 如果是空,就给当前节点构建一个左子树(down)和一个右子树(up)
node.left = new Node("down", null, null);
node.right = new Node("up", null, null);
}
}
}
}
return root;
}
// 定义结点类
private static class Node {
public String item;
public Node left;
public Node right;
public Node(String item, Node left, Node right) {
this.item = item;
this.left = left;
this.right = right;
}
}
//存放节点的队列
private static class PaperQueue {
//首结点
private QueueNode head;
//当前队列的元素个数
private int n;
//记录最后一个结点
private QueueNode last;
public PaperQueue() {
head = new QueueNode(null, null);
last = null;
n = 0;
}
//判断队列是否为空
public boolean isEmpty() {
return n == 0;
}
//从队列中拿出一个元素
public Node dequeue() {
if (isEmpty()) {
return null;
}
// 不是空,出列
// 获取当前的第一个元素(对应图中的1元素)
QueueNode oldFirst = head.next;
// 让head结点指向下一个结点(对应图中的2元素)
head.next = head.next.next;
// 个数-1
n--;
if (isEmpty()) {
last = null;
}
return oldFirst.item;
}
//往队列中插入一个元素
public void enqueue(Node t) {
// 判断last是否为null
if (last == null) {
// last为空,要插入的元素就是last
last = new QueueNode(t, null);
// 让首结点指向last
head.next = last;
} else {
// 不是第一个元素
// 取出旧结点(last)
QueueNode oldLast = last;
// 创建新的结点给last
last = new QueueNode(t, null);
// 让旧的last元素指向新的结点
oldLast.next = last;
}
// 个数+1
n++;
}
private class QueueNode {
public Node item;
public QueueNode next;
public QueueNode(Node item, QueueNode next) {
this.item = item;
this.next = next;
}
}
}
}





评论区