概述
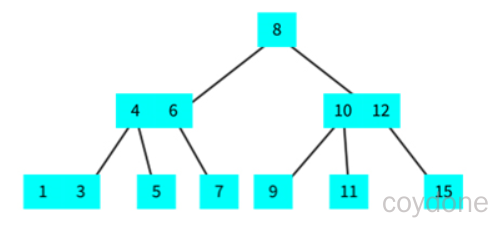
为了保证查找树的平衡性,需要一些灵活性,因此允许树中的一个结点保存多个键。确切的说,将一棵标准的二叉查找树中的结点称为2-结点(含有一个键和两条链),而现在引入3-结点,它含有两个键和三条链。2-结点和3-结点中的每条链都对应着其中保存的键所分割产生的一个区间。
一棵2-3查找树要么为空,要么满足下面两个要求:
-
2-结点:含有一个键(及其对应的值)和两条链,左链接指向2-3树中的键都小于该结点,右链接指向的2-3树中的键都大于该结点。
-
3-结点:含有两个键(及其对应的值)和三条链,左链接指向的2-3树中的键都小于该结点,中链接指向的2-3树中的键都位于该结点的两个键之间,右链接指向的2-3树中的键都大于该结点。
查找
将二叉查找树的查找算法一般化就能够直接得到2-3树的查找算法。要判断一个键是否在树中,我们先将它和根结点中的键比较。如果它和其中任意一个相等,查找命中;否则我们就根据比较的结果找到指向相应区间的连接,并在其指向的子树中递归地继续查找。如果这个是空链接,查找未命中。
插入
插入元素首先进行查找命中,若查找命中则不予插入此元素,如果需要支持重复的元素则将这个元素对象添加一个属性count。若查找未命中,则在叶子节点中插入这个元素。
空树的插入很简单,创建一个节点即可。如果不是空树,插入的情况分为以下几种:
1、向2-节点中插入元素;
如果未命中查找结束于2-节点,直接将2-节点替换为3-节点,并将待插入元素添加到其中。
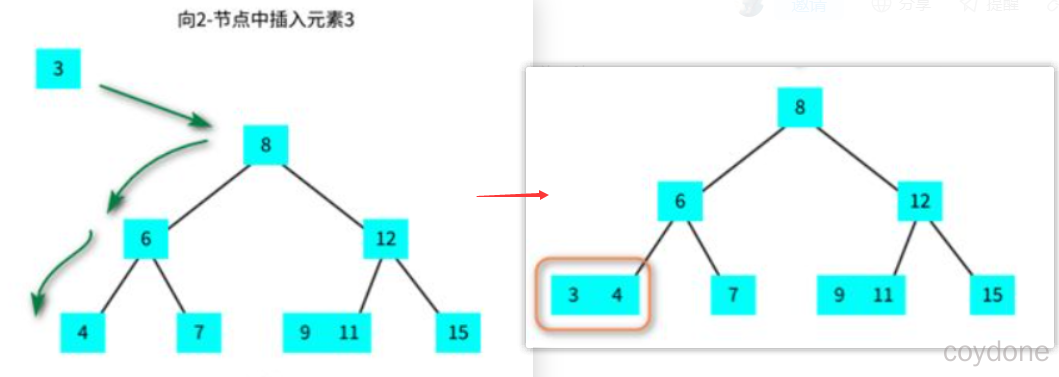
2、向一颗只含有一个3-节点的树中插入元素;
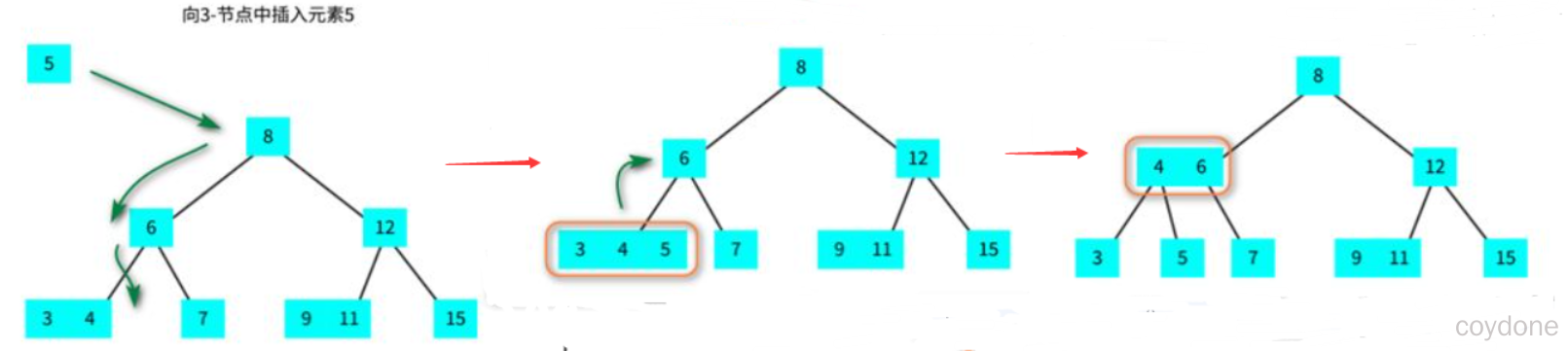
如果命中查找结束于3-节点,先临时将其成为4-节点,把待插入元素添加到其中,然后将4-节点转化为3个2-节点,中间的节点成为左右节点的父节点。如果之前临时4-节点有父节点,就会变成向一个父节点为2-节点的3-节点中插入元素,中间节点与父节点为2-节点的合并。
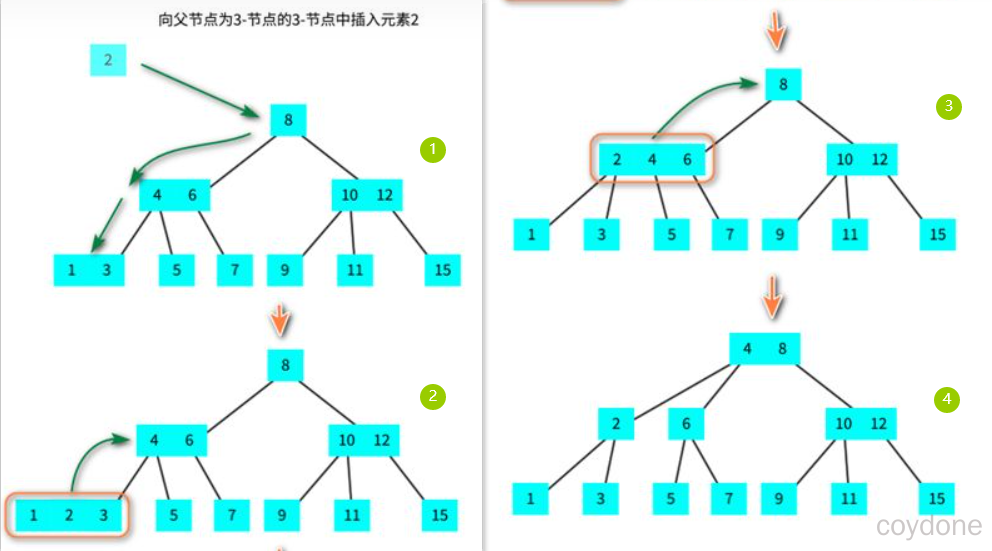
3、向一个父节点为2-节点的3-节点中插入元素;
和上面的情况一样,我们也可以将新的元素插入到3-结点中,使其成为一个临时的4-结点,然后,将该结点中的中间元素提升到父结点即2-结点中,使其父结点成为一个3-结点,然后将左右结点分别挂在这个3-结点的恰当位置。
4、向一个父节点为3-节点的3-节点中插入元素。
插入元素后一直向上分解临时的4-节点,直到遇到2-节点的父节点变成3-节点不再分解。如果达到树根节点还是4-节点,则分解根节点,此时树高+1(只有分解根节点才会增加树高)。
通过对2-3树插入操作的分析,发现在插入的时候,2-3树需要做一些局部的变换来保持2-3树的平衡。一棵完全平衡的2-3树具有以下性质:
-
任意空链接到根结点的路径长度都是相等的。
-
4-结点变换为3-结点时,树的高度不会发生变化,只有当根结点是临时的4-结点,分解根结点时,树高+1。
-
2-3树与普通二叉查找树最大的区别在于,普通的二叉查找树是自顶向下生长,而2-3树是自底向上生长。
直接实现2-3树比较复杂,因为需要处理不同的结点类型,非常繁琐; 需要多次比较操作来将结点下移; 需要上移来拆分4-结点; 拆分4-结点的情况有很多种;2-3查找树实现起来比较复杂,在某些情况插入后的平衡操作可能会使得效率降低。
2-3树实现
API设计
数据结点
类名:Data
构造方法 public Data(Integer key, String value)
成员方法 public void print() 输出数据
成员属性 private Integer key; 存储键
private String value; 存储值
树结点
类名:Node
成员属性
private static final int N = 3;
private Node parent;// 该结点的父节点
//子节点,子节点有3个,分别是左子结点,中间子结点和右子结点
private Node[] chirldNodes = new Node[N];
//代表结点保存的数据(为一个或者两个)
private Data[] itemDatas = new Data[N-1];
private int itemNum = 0;// 结点保存的数据个数
成员方法
public void print() //输出数据
private boolean isLeaf() // 判断节点是否是叶子结点
private boolean isFull()//判断节点存储数据是否满了
private Node getParent()// 返回该节点的父节点
private void connectChild(int index, Node child)//连接子节点。0左1中2右
private Node disconnectChild(int index)//解除该节点与某个节点之间的连接
private Data getData(int index)// 获取节点左或右的键值对,0左1右
private Node getChild(int index)//获取某位置的子树
public int getItemNum()// 返回结点中键值对的数量,空则返回-1
private int findItem(Integer key)//寻找key在结点的位置
private int insertData(Data data)//向结点插入键值对:前提是结点未满
private Data removeItem()
2-3树类名:Tree23
构造方法:public Tree23()
成员属性
private Node root;
private int n;
成员方法
public int size()//树的大小
public boolean isEmpty()//树是否为空
public String find(Integer key)// 查找含有key的键值对
//在key的条件下获得结点的子节点(可能为左子结点,中间子节点,右子节点)
private Node getNextChild(Node node, Integer key)
public void insert(Integer key, String value)// 插入
private void split(Node node, Data data)//裂变节点
private void connectNode(Node parent, Node node)//连接node和parent
代码实现
public class Tree23 {
//根结点
private Node root;
//元素个数
private int n;
public Tree23() {
root = new Node();
n = 0;
}
//返回树的大小
public int size() {
return n;
}
//判断树是否为空
public boolean isEmpty() {
return n == 0;
}
/**
* 查找含有key的键值对
* @param key
* @return 返回键值对中的value
*/
public String find(Integer key) {
// 获取根节点
Node currentNode = root;
int childNum;
while (true) {
if ((childNum = currentNode.findItem(key)) != -1) {
// 说明key存在
return currentNode.itemDatas[childNum].value;
} else if (currentNode.isLeaf()) {
// 如果当前节点不是要查询的key,并且没有叶子结点
return null;
} else {
// 当前节点不是要查询的key,并且有叶子结点
currentNode = getNextChild(currentNode, key);
}
}
}
/**
* 在key条件下获取指定节点的子节点。
* @param node
* @param key
* @return 返回子节点
*/
private Node getNextChild(Node node, Integer key) {
for (int i = 0; i < node.getItemNum(); i++) {
if (node.getData(i).key > key) {
// 指定节点的key大于我们的key
return node.getChild(i);
} else if (node.getData(i).key.equals(key)) {
// 直接返回node
return node;
}
}
// 没有找到,直接返回子节点的右节点/中节点/左节点
return node.getChild(node.getItemNum());
}
/**
* 插入数据到2-3查找树
* @param key
* @param value
*/
public void insert(Integer key, String value) {
// 创建一个要插入的节点
Data data = new Data(key, value);
// 获取根节点
Node currentNode = root;
while (true) {
if (currentNode.isLeaf()) {
break;
} else {
// 不是叶子节点
// 获取下一个子节点
currentNode = getNextChild(currentNode, key);
// 遍历当前节点,找到需要替换的位置
for (int i = 0; i < currentNode.getItemNum(); i++) {
if (currentNode.getData(i).key.equals(key)) {
// 赋值
currentNode.getData(i).value = value;
return;
}
}
}
}
// 遍历完了,执行到了这里,说明key不存在
// 如果要插入的key的节点已经满了,即3-结点插入
if (currentNode.isFull()) {
split(currentNode, data);
} else {
// 2-结点插入
currentNode.insertData(data);
}
}
/**
* 裂变方法,用于裂变节点,该过程并不是要基于现有节点改造
* 而是构造一个新的节点去替换
* @param node 被裂变的结点
* @param data 要保存的键值对
*/
private void split(Node node, Data data) {
Node parent = node.getParent();
// 用于存放最大节点
Node maxNode = new Node();
// 用于存放最小结点
Node midNode = new Node();
if (data.key < node.getData(0).key) {
maxNode.insertData(node.removeItem());
midNode.insertData(node.removeItem());
node.insertData(data);
} else if (data.key < node.getData(1).key) {
// 介于0和1之间
maxNode.insertData(node.removeItem());
midNode.insertData(data);
} else {
midNode.insertData(node.removeItem());
maxNode.insertData(data);
}
if (node == root) {
root = midNode;
}
midNode.connectChild(0, node);
midNode.connectChild(1, maxNode);
connectNode(parent, midNode);
}
/**
* 连接node和parent,该过程并不是要基于现有节点改造,而是构造一个新的节点去替换
* @param parent
* @param node
*/
private void connectNode(Node parent, Node node) {
// 要合并的节点的最左边的节点
Data data = node.getData(0);
if (node == root) {
return;
}
// 父节点是3-节点
if (parent.isFull()) {
Node gParent = parent.getParent();
Node newNode = new Node();
Node temp1, temp2;
Data itemData;
if (data.key < parent.getData(0).key) {
temp1 = parent.disconnectChild(1);
temp2 = parent.disconnectChild(2);
newNode.connectChild(0, temp1);
newNode.connectChild(1, temp2);
newNode.insertData(parent.removeItem());
itemData = parent.removeItem();
parent.disconnectChild(2);
parent.insertData(itemData);
parent.connectChild(0, node);
parent.connectChild(1, newNode);
} else if (data.key < parent.getData(1).key) {
temp1 = parent.disconnectChild(0);
temp2 = parent.disconnectChild(2);
Node tempNode = new Node();
newNode.insertData(parent.removeItem());
newNode.connectChild(0, node.disconnectChild(1));
newNode.connectChild(1, temp2);
tempNode.insertData(parent.removeItem());
tempNode.connectChild(0, temp1);
tempNode.connectChild(1, node.disconnectChild(0));
parent.insertData(node.removeItem());
parent.connectChild(0, tempNode);
parent.connectChild(1, newNode);
} else {
itemData = parent.removeItem();
newNode.insertData(parent.removeItem());
newNode.connectChild(0, parent.disconnectChild(0));
newNode.connectChild(1, parent.disconnectChild(1));
parent.insertData(itemData);
parent.connectChild(0, newNode);
parent.connectChild(1, node);
}
// 进行递归
connectNode(gParent, parent);
} else {
Node temp1, temp2;
if (data.key < parent.getData(0).key) {
Node tempNode = parent.disconnectChild(1);
temp1 = node.disconnectChild(0);
temp2 = node.disconnectChild(1);
parent.insertData(node.getData(0));
parent.connectChild(0, temp1);
parent.connectChild(1, temp2);
parent.connectChild(2, tempNode);
} else {
parent.connectChild(1, node.disconnectChild(0));
parent.connectChild(2, node.disconnectChild(1));
parent.insertData(node.getData(0));
}
}
}
public void print() {
root.print();
}
private static class Node {
private static final int N = 3;
//父节点
public Node parent;
/**
* 子节点
* 0代表左节点
* 1代表中节点
* 2代表右节点
*/
public Node[] childNodes = new Node[N];
//结点保存的数据
public Data[] itemDatas = new Data[N - 1];
//节点保存的数据个数
public int itemCount = 0;
//输出数据
public void print() {
for (int i = 0; i < itemCount; i++) {
itemDatas[i].print();
}
System.out.println("/");
}
/**
* 判断节点是否是叶子结点
* 只要没有子节点,就是叶子结点
* @return
*/
private boolean isLeaf() {
return childNodes[0] == null;
}
/**
* 判断节点数据是否存满
* 只要itemCount的大小是2,那么就是存满了
* @return
*/
private boolean isFull() {
return itemCount == N - 1;
}
//返回该节点的父节点
private Node getParent() {
return parent;
}
/**
* 连接子节点
* @param index 连接的位置(0代表左子树,1代表中子树,2代表右子树)
* @param child 要连接的节点
*/
private void connectChild(int index, Node child) {
childNodes[index] = child;
// 判断如果child不为空,指定一下父节点
if (child != null) {
child.parent = this;
}
}
/**
* 解除该节点与某个子节点之间的练习
* @param index 连接的位置(0代表左子树,1代表中子树,2代表右子树)
* @return 解除的节点
*/
private Node disconnectChild(int index) {
Node temp = childNodes[index];
childNodes[index] = null;
return temp;
}
/**
* 获取结点的左或右键值对
* @param index 0左 1右
* @return
*/
private Data getData(int index) {
return itemDatas[index];
}
/**
* 获取某位置的子树
* @param index 连接的位置(0代表左子树,1代表中子树,2代表右子树)
* @return
*/
private Node getChild(int index) {
return childNodes[index];
}
/**
* 返回节点中键值对的数量
* @return
*/
public int getItemNum() {
return itemCount;
}
/**
* 寻找key在结点的位置
* @param key
* @return 如果不存在就返回-1
*/
private int findItem(Integer key) {
for (int i = 0; i < itemCount; i++) {
if (itemDatas[i] == null) {
break;
} else if (itemDatas[i].key.equals(key)) {
return i;
}
}
return -1;
}
/**
* 向结点插入键值对,前提是节点未满
* @param data
* @return 插入后的坐标
*/
private int insertData(Data data) {
itemCount++;
for (int i = N - 2; i >= 0; i--) {
if (itemDatas[i] == null) {
continue;
} else {
if (data.key < itemDatas[i].key) {
// 要插入的数据小于当前的key
// 当前的key向右移,要插入的数据插入到现有位置
itemDatas[i + 1] = itemDatas[i];
} else {
// 不小于,直接插入到右边
itemDatas[i + 1] = data;
return i + 1;
}
}
}
itemDatas[0] = data;
return 0;
}
/**
* 移除最后一个键值对(有右边的键值对就移除右边的,否则就移除左边的)
* @return 移除后的键值对
*/
private Data removeItem() {
// 获取最右边的数据
Data temp = itemDatas[itemCount - 1];
itemDatas[itemCount - 1] = null;
itemCount--;
return temp;
}
}
//数据节点
private static class Data {
public Integer key;
public String value;
public Data(Integer key, String value) {
this.key = key;
this.value = value;
}
public void print() {
System.out.println("/" + key + "---" + value);
}
}
}





评论区