图的定义及分类

图是由一组顶点和一组能够将两个顶点相连的边组成的。在计算机科学中，一个图就是一些顶点的集合，这些顶点通过一系列边结对（连接）。顶点用圆圈表示，边就是这些圆圈之间的连线。顶点之间通过边连接。（顶点有时也称为节点或者交点，边有时也称为链接）

图有各种形状和大小。边可以有权重（weight），即每一条边会被分配一个正数或者负数值。

边可以是有方向的。

树和链表可以被当成是图，只不过是一种更简单的形式。它们都有顶点（节点）和边（连接）。

图可以包含圈（cycles），即你可以从一个顶点出发，沿着一条路径最终会回到最初的顶点。树是不包含圈的图。

另一种常见的图类型是单向图或者 DAG：就像树一样，这个图没有任何圈（无论你从哪一个节点出发，你都无法回到最初的节点），但是这个图有有向边（通过一个箭头表示，这里的箭头不表示继承关系）。

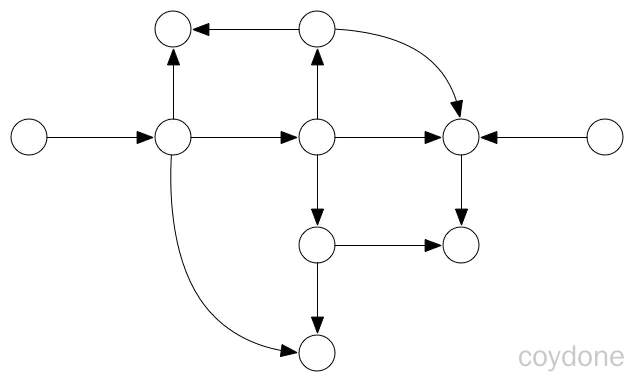
特殊的图：

自环：即一条连接一个顶点和其自身的边；
平行边：连接同一对顶点的两条边；

按照连接两个顶点的边的不同，可以把图分为以下两种：

无向图：边仅仅连接两个顶点，没有其他含义；
有向图：边不仅连接两个顶点，并且具有方向；

图的表示方式

理论上，图就是一堆顶点和边对象而已，在代码中通过邻接列表和邻接矩阵来描述。

邻接列表：在邻接列表实现中，每一个顶点会存储一个从它这里开始的边的列表。比如，如果顶点A 有一条边到B、C和D，那么A的列表中会有3条边。

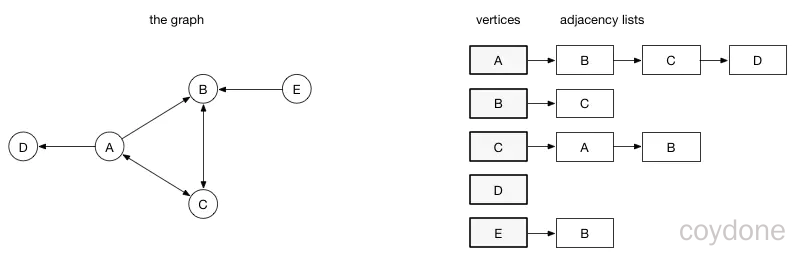
邻接列表只描述了指向外部的边。A 有一条边到B，但是B没有边到A，所以 A没有出现在B的邻接列表中。查找两个顶点之间的边或者权重会比较费时，因为遍历邻接列表直到找到为止。

**邻接矩阵：**在邻接矩阵实现中，由行和列都表示顶点，由两个顶点所决定的矩阵对应元素表示这里两个顶点是否相连、如果相连这个值表示的是相连边的权重。例如，如果从顶点A到顶点B有一条权重为 5.6 的边，那么矩阵中第A行第B列的位置的元素值应该是5.6：

往这个图中添加顶点的成本非常昂贵，因为新的矩阵结果必须重新按照新的行/列创建，然后将已有的数据复制到新的矩阵中。

大多数时候，选择邻接列表是正确的。下面是两种实现方法更详细的比较。

假设 V 表示图中顶点的个数，E 表示边的个数。

操作	邻接列表	邻接矩阵
存储空间	O(V + E)	O(V^2)
添加顶点	O(1)	O(V^2)
添加边	O(1)	O(1)
检查相邻性	O(V)	O(1)

“检查相邻性” 是指对于给定的顶点，尝试确定它是否是另一个顶点的邻居。在邻接列表中检查相邻性的时间复杂度是O(V)，因为最坏的情况是一个顶点与每一个顶点都相连。

在稀疏图的情况下，每一个顶点都只会和少数几个顶点相连，这种情况下相邻列表是最佳选择。如果这个图比较密集，每一个顶点都和大多数其他顶点相连，那么相邻矩阵更合适。

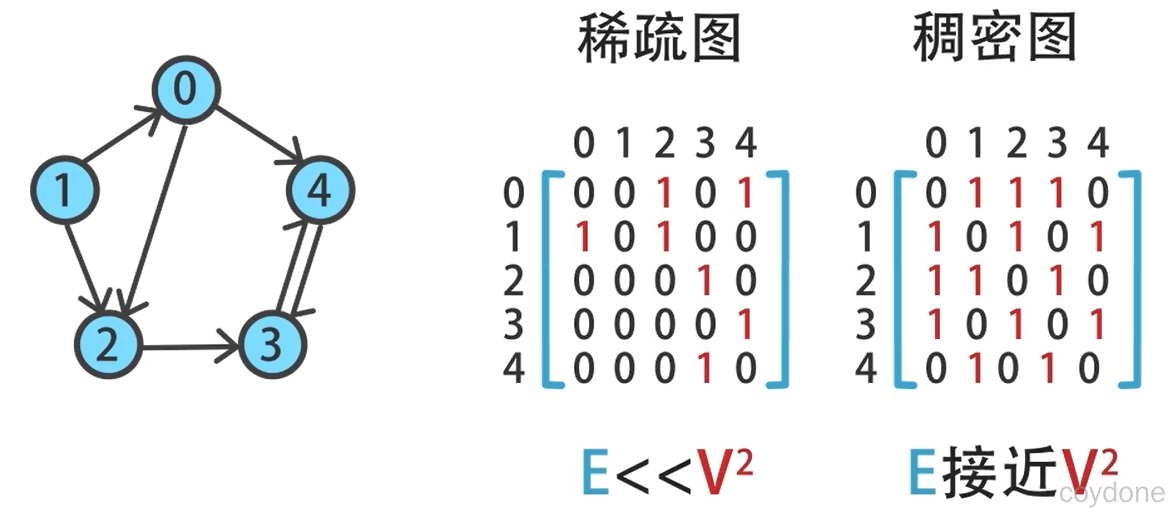
一般用邻接表表示稀疏图，用邻接矩阵表示稠密图。

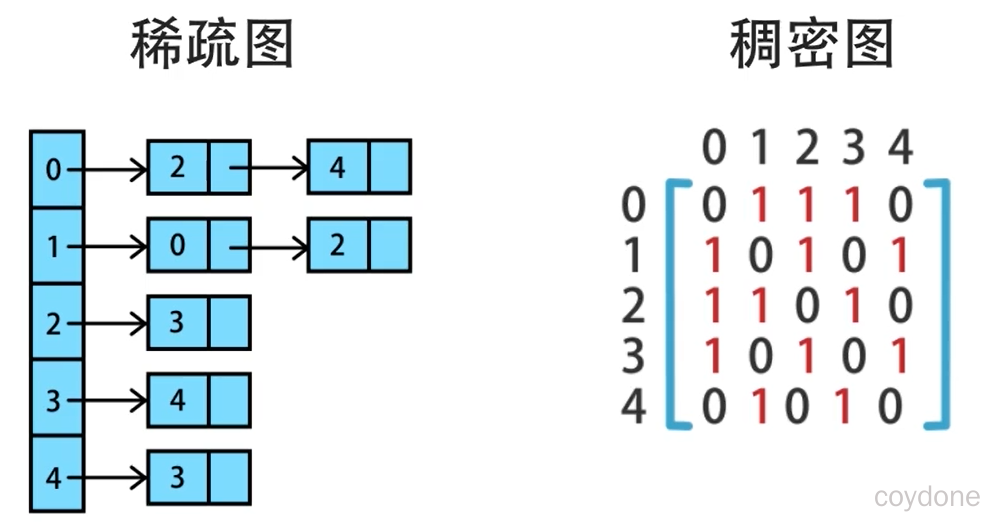
无向图的实现

API设计

类名 Graph
构造方法 Graph(int V)：创建一个包含V个顶点但不包含边的图
成员方法
	public int V()：获取图中顶点的数量
	public int E()：获取图中边的数量
	public void addEdge(int v,int w)：向图中添加一条边 v-w
	public Queue adj(int v)：获取和顶点v相邻的所有顶点
成员变量
	private int V：记录顶点数量
	private int E：记录边数量
	private Queue[] adj： 邻接表

代码实现

import java.util.Queue;
import java.util.concurrent.ArrayBlockingQueue;

public class Graph {

    //顶点数量
    private int v;

    //边数量
    private int e;

    //邻接表
    private Queue<Integer>[] adj;

    //创建一个包含V个顶点但不包含边的图
    public Graph(int v) {
        // 初始化顶点数量
        this.v = v;
        // 初始化边的数量
        this.e = 0;
        // 初始化邻接表
        this.adj = new Queue[v];
        // 初始化邻接表中的空队列
        for (int i = 0; i < adj.length; i++) {
            adj[i] = new ArrayBlockingQueue<>(5);
        }
    }

    //获取图中定点的数量
    public int V() {
        return v;
    }

    //获取图中边的数量
    public int E() {
        return e;
    }

    //向图中添加一条边v-w
    public void addEdge(int v, int w) {
        // 把w添加到v的链表中，这样顶点v就多了一个相邻点w
        adj[v].add(w);
        // 把v添加到w的链表中，这样顶点w就多了一个相邻的点v
        adj[w].add(v);
        // 边的数量自增1
        e++;
    }

    //获取和顶点v相邻的所有顶点
    public Queue adj(int v) {
        return adj[v];
    }

    //测试
    public static void main(String[] args) {
        Graph graph = new Graph(5);
        graph.addEdge(0, 1);
        graph.addEdge(0, 2);
        graph.addEdge(1, 2);
        graph.addEdge(2, 3);
        graph.addEdge(3, 4);
        graph.addEdge(0, 4);
		//new DepthFirstSearch(graph,0);
    }
}

图的搜索

深度优先搜索

所谓的深度优先搜索（Depth-First Search，简称DFS），指的是在搜索时，如果遇到一个结点既有子结点，又有兄弟结点，那么先找子结点，然后找兄弟结点。

public class DepthFirstSearch {
    //记录有多少个顶点与S顶点相通
    private int count;
    //索引代表顶点，值代表当前顶点是否已经被搜索
    private boolean[] marked;

    //构造深度优先搜索对象，使用深度优先搜索出图中s顶点的所有相通顶点
    public DepthFirstSearch(Graph g, int s) {
        // 构造一个和图大小一样的布尔数组
        marked = new boolean[g.V()];
        // 构造g图中与顶点s相通的所有顶点
        dfs(g, s);
    }

    //使用深度优先搜索找出g图中v定点的所有相通顶点
    private void dfs(Graph g, int v) {
        System.out.println(v);
        // 当前节点标记为已搜索
        marked[v] = true;
        // 遍历v定点的邻接表，找到每一个顶点w
        Queue<Integer> queue = g.adj(v);
        for (Integer w : queue) {
            // 如果当前顶点w没有被搜索过，则递归搜索与w顶点相通的其他顶点
            if (!marked[w]) {
                dfs(g, w);
            }
        }
        // 相通的顶点数量+1
        count++;
    }

    //判断w顶点与s顶点是否相通
    public boolean marked(int w) {
        return marked[w];
    }

    public int count() {
        return count;
    }
}

广度优先搜索

所谓的广度优先搜索（Breadth-First Search，简称BFS），指的是在搜索时，如果遇到一个结点既有子结点，又有兄弟结点，那么先找兄弟结点，然后找子结点。

import java.util.Queue;
import java.util.concurrent.ArrayBlockingQueue;

public class BreadthFirstSearch {

    //索引代表顶点，值代表当前顶点是否已经被搜索
    private boolean[] marked;

    //记录有多少个顶点与s顶点想通
    private int count;

    //存储待搜索邻接表的点
    private Queue<Integer> waitSearch;

    //使用广度优先搜索找出G图中v顶点的所有相邻顶点
    public BreadthFirstSearch(Graph g, int v) {
        // 构造一个和图大小一样的布尔数组
        marked = new boolean[g.V()];
        // 初始化待搜索顶点的队列
        waitSearch = new ArrayBlockingQueue<>(g.V());
        // 构造g图中与顶点s相通的所有顶点
        bfs(g, v);
    }

    //使用广度优先搜索找出g图中v顶点的所有相邻顶点
    private void bfs(Graph g, int v) {
        // 把当前顶点v放入到队列中，等待搜索它的邻接表
        waitSearch.offer(v);
        // 使用while循环从队列中取出待搜索的顶点wait，进行搜索邻接表
        while (!waitSearch.isEmpty()) {
            Integer wait = waitSearch.poll();
            // 把wait设为已搜索
            marked[wait] = true;
            System.out.println(wait);
            // 遍历wait顶点的邻接表，得到每一个顶点
            Queue<Integer> queue = g.adj(wait);
            for (Integer w : queue) {
                // 如果当前顶点w没有被搜索，则递归搜索与w想通的其他顶点
                if (!marked[w] && !waitSearch.contains(w)) {
                    waitSearch.offer(w);
                }
            }
        }
        count++;
    }

    //判断w顶点与s顶点是否相通
    public boolean marked(int w) {
        return marked[w];
    }

    public int count() {
        return count;
    }
}

目录CONTENT

图